年最大日雨量の超過確率について

三重県林業研究所　野々田　稔　郎

◆はじめに

　平成23年台風12号は、紀伊半島全域に、深層崩壊や洪水を発生させ、大きな被害をもたらしました。三重県では、過去にも豪雨に伴う斜面崩壊等の山地災害が発生しています。昭和34年伊勢湾台風、昭和57年台風10号、平成16年台風21号等は、いずれも豪雨により大きな被害を発生させました。これらの災害誘因となる豪雨については、従来から「超過確率雨量」、「X年確率雨量」等により、統計的にその雨量の大きさの比較や将来予測が行われています。ここでは、この確率雨量について説明します。

◆降雨量の地域性

　図-1は、津地方気象台の津観測点と尾鷲観測点の観測データを用いて、1939～2011年の年最大日雨量（1年間の日雨量の最大値）を年別に示しています。多雨地域である尾鷲の年最大日雨量は、津より全体的に大きく、全期間の平年値は尾鷲348mmで、津140mmの約2.5倍の値です。尾鷲では350mmの年最大日雨量が毎年降る程度の雨である一方で、津では、かなり大きい雨量であることを示しています。

　年最大日雨量は、期間1年の最大値であり、決して小さい雨量ではありませんが、山地災害の発生から350mmの日雨量を考えると、尾鷲地域では毎年発生する程度の雨で、大災害を誘発する可能性は小さいと考えられます。一方、平年値140mmの津地域では、大きな災害を誘発する可能性が考えられます。

　したがって、災害発生に関係する降雨の大きさは、単に降雨量（mm）ではなく、その地域の降雨特性を考慮し、判断する必要があります。
　　　
　　図-1 年最大日雨量（1939年～2011年データ）
　　　　*:津地方気象台観測データに基づき図示

◆年最大日雨量の頻度分布

　図－2は、津観測点における1901～2011年の年最大日雨量データを用いた頻度分布図です。最頻値は階級値100mm（80～120mm階級）で全体の約40％を占めています。年最大日雨量や最小日雨量等の極値の頻度分布は、対数正規分布型となることが知られ、左右対称の正規分布と異なり、一般に最頻値が左側にずれ、右側の裾野が広くなる分布型を示します。観測データから対数正規分布関数を求め、実線で図示すると、ほぼ頻度分布の再現が可能でした。

　頻度分布を対数正規分布関数で再現可能であると、縦軸の頻度は、年最大日雨量の発生確率を表し、模式的には図-3のとおりです。同図の雨量P(mm)より大きい年最大日雨量が発生する確率が雨量Pの超過確率であり、その確率は、雨量Pより大きい発生確率の総和（斜線部の面積）から得られます。Pより小さい雨量発生の確率が雨量Pの非超過確率であり、同様にPより小さい確率の総和（白抜きの面積）がその確率です。雨量Pの非超過確率f(P)と超過確率W(P)は以下の関係があります。

　　　　W (P ) ＝ 1 – f (P )　････････　　　(1)　
　　　　
　　図-2 年最大日雨量の頻度分布（観測点：津）
　　
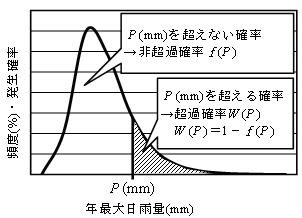
　　図-3 年最大日雨量の確率分布（対数正規分布）

◆対数正規確率紙を用いた（非）超過確率等の作図法

　観測データから(非)超過確率を求める方法は、岩井法、石原・高瀬法、ガンベル・チョー法等種々提案されています。ここでは、簡便な対数正規確率紙を用いる作図法により、津、尾鷲の観測データから、年最大日雨量の超過確率等を求めてみます。確率紙は、観測データと非超過確率をプロットできるように作成されたグラフ用紙で、正規、対数正規、指数等があり、表計算ソフトでも作成が可能です。

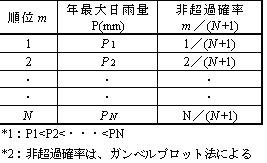
　まず、表-1に示すように、観測値を小さい順に並べ、それぞれの観測値に対する非超過確率を求めます。表に示すように、非超過確率は観測値の順位とデータ数Nから計算できます。

　図-4が対数正規確率紙にプロットした津観測点（1901～2011年、N=111）、尾鷲観測点（1939年～2011年、N=73）のデータです。横軸は年最大日雨量（対数目盛）、縦軸は非超過確率（100分率表示）であり、横軸を対数とせず、通常目盛とすれば正規分布に対応した正規確率紙となります。

　　　表-1 年最大日雨量の非超過確率

◆年最大日雨量の（非）超過確率、再現確率等の計算

　図-4の津（●）、尾鷲（■）に引いた実線は各観測点に対応する回帰線であり、いずれも高い相関性が認められます。年最大日雨量Pと非超過確率f (P)は、以下の式形で表されます（a、b定数）。

　　f (P)＝ a･ln (P) ＋ b　････････　　(2)

　同図に示すように、津のデータに比べ、年最大日雨量が大きい尾鷲のデータは全体的に右側にプロットされています。非超過確率90％に対応する年最大日雨量（回帰線との交点）を求めると、津209mm、尾鷲529mmとなります。非超過確率90％は、(1)式より、超過確率10％（10=100－90）であるので、確率年は1／10となり、津209mm、尾鷲529mmを超える日雨量は、それぞれの地域において、10年に一度程度の確率で発生すると推定されます。また、200mmの日雨量は、観測点別に津の超過確率12.1％、再現確率年8.3年、尾鷲の超過確率89.9％、再現確率年1.1年が計算できます。

　図-5は、対数正規確率紙にプロットした津観測点のデータですが、111年間のデータを1901～1955年（55年間）のデータと、最近の56年間（1956～2011年）のデータに分けて示しています。最近の56年間のデータの回帰線は、それ以前のデータに比べ、右側にプロットされています。回帰線を用いて、再現確率100年（非超過確率99％、超過確率1％）の日雨量を求めると、1901～1955年：287mm、1956～2011年：366mmとなり、年最大日雨量は、最近の56年間の観測値が、それ以前より大きい傾向を示しました。

　今後、この傾向がより顕著となるかどうかはよく解りませんが、近年、雨の降り方が変わったと言われ、感覚的にも頷けるところです。短時間で強度の大きい雨が降るゲリラ豪雨はその例です。また、津観測点における2004年台風21号（宮川災害）の日雨量（427mm）は、111年間のデータの中でも破格に大きく、これを除くと、再現確率は2000年に1回程度の大雨である計算になります。今後、このような豪雨が頻発する可能性は極めて低いと考えられますが、山地災害に備え、治山施設の充実や森林整備の推進等の防災対策が重要であると思われます。
　　
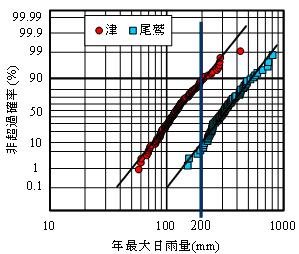
　　　　図-4 年最大日雨量と非超過確率の関係
　　
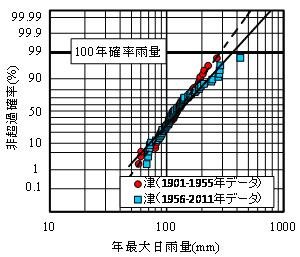
　図-5　津観測点の年最大日雨量と非超過確率の関係

　（1901～1955年と1956～2011年データを分けて計算）