過密人工林の樹幹細り形状
三重県林業研究所 野々田 稔 郎
完満(カンマン)と梢殺(ウラゴケ)
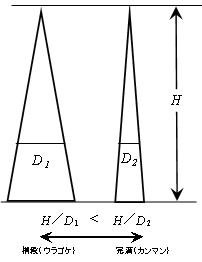
木の樹幹が先端ほど細くなるのはご存じのとおりです。この樹幹の細りの程度をあらわす言葉として完満(カンマン)と梢殺(ウラゴケ)があります。樹幹の細りが大きいものを梢殺と言い、細りの小さいものを完満であると表現されます。さて、完満と梢殺といった表現は、同程度のサイズの樹木Aと樹木Bを比較した相対的な判断には有効です。しかし、樹高や直径の異なった多数の樹木(または丸太)を対象とする場合に、その細りの程度を何らかの基準値で比較する必要があります。簡便な判断基準の一つに、樹高Hと胸高直径Dを用いて、H/Dによって求める形状比があります。すなわち、図-1に示すように、形状比が大きいほど完満、小さいほど梢殺です。
樹高成長は土地生産力(地位)の影響が大きく、森林施業によってその成長をコントロールすることは難しいとされています。これに対し、直径成長は密度の影響が大きく、植栽本数、間伐の方法等によって、ある程度その成長をコントロールすることが可能です。したがって心持ち柱材を生産目標とする林業地では、密植、弱度の間伐を頻繁に行うことによって、採材効率等が良い完満な材を生産してきました。一方、板材を生産目標とする林業地では、疎植で肥大成長に主眼をおいた施業が行われ、結果として梢殺の強い樹幹形を作り上げてきたことになります。これらは、生産目標に応じて施業方法(特に密度管理)の違いによる結果と言えます。
|
図-1 樹幹の模式図 |
細り形状を表す「細り表」
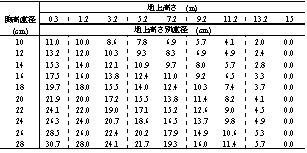
樹幹形を形状比によってある程度判断できることを述べましたが、より詳細な樹幹の細り形状を把握することは、立木の丸太材積推定や採材のための径級把握等において有用な情報です。また、近年では間伐の推進が重要な施策となっていますが、材積ベースでの間伐率の算定や間伐材の利用径級の判断等をより正確に把握するために重要な資料であると考えられます。このため,実測値に基づいた樹幹の細り形状を一覧表にまとめた「細り表」がいくつかの地域で作成されています。表-1はヒノキ(樹高15m)の細り表の一例ですが、樹幹の各胸高直径の地上高さ別直径が表から読み取れます。例えば、同表にしたがうと、樹高15m、胸高直径16cmの樹幹の地上高さ7.2mの直径は11.0cmであることがわかります。「細り表」は樹幹の細り程度の把握や採材計画の立案等において有用であろうと考えられますが、三重県では作成されていないのが現状です。
表-1 ヒノキ(樹高15m)の細り表の例
ヒノキ樹幹の細り形状
そこで、いくつかの林分から試験木を採取し、樹幹の細り形状を測定してみました。ここでは、ヒノキ(6林分、43本)の例を示します。測定したヒノキ林の林齢はいずれも35年生前後であり、林内には枯死木が見られ、今後間伐の必要があると判断される過密林分です(したがって、樹幹は完満であることが予測される)。試験木を伐倒した後に、地上0.3m、1.2m、2.2m・・・・・梢端までの高さで円板を採取し、その直径を測定しました。
図-2は、測定した試験木のうち、個体サイズの大、中、小の例を示したものです。図は原点が樹幹の梢端の位置を表し、横軸は梢端からの距離、縦軸は直径をそれぞれ表しています。ドット(○、△、□)は採取した円板の実測値を示し(最も梢端からの距離が大きい実測値は地上0.3mの円板)、曲線は実測値に当てはめを行った幹曲線です。地際の根張りの箇所でやや過小となっているのを除けば、実測値とよく適合し、樹幹の細り形状をほぼ再現しています。

図-2 樹幹細り測定結果と幹曲線の当てはめ例
幹曲線の推定には幹曲線式が用いられ,現在までクンツェ(KUNZE)式,ベーレ(BEHRE)式,多項式(3次式の場合は吉田式)など多くの式が提案されています。ここでは、以下に示す多項式を用いました。多項式を用いる理由は、①実測値に柔軟に適合させやすいこと,②積分が容易で材積を求めやすいこと,③データへの当てはめにあたって市販の表計算ソフトを用いて最小二乗法による適合性の検討を簡便に行える等の長所があるからです。
di = a
ここに,di :樹皮内直径,l
幹曲線の相対化と統合
図-3は、図-2に示した樹幹の細り形状を相対化して示しています。相対化とは、相対梢端距離を(1)式中の梢端距離/樹高により(l
D
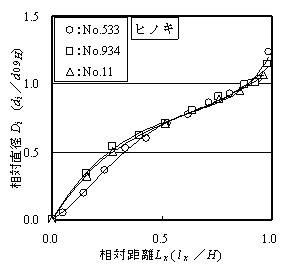
図-3 相対化した樹幹細り形状
さて、相対幹曲線は、樹種、生育環境、林齢等が同程度であれば、サイズの異なる樹幹の形状をほぼ一つの線で表現できることが知られています。そこで、今回測定したヒノキ6林分(林齢35年生前後で、何れも本数密度が高い林分)のデータを全て相対化したところ、図-4の○に示すように個体サイズが異なっても、比較的ばらつきが小さく表すことができました。これらのデータから求めた幹曲線(上の(2)式)が図中の実線であり、これらのデータを統合した代表的な幹曲線と考えても良さそうです。なお、(2)式中の係数は=1.30800、a

図-4 統合した相対幹曲線